| Stepper Motor Holding Torque |
The holding torque of a stepper motor can be approximated by analyzing the step response of the motor. Whenever a stepper motor is stepped, it resonates at a frequency of:
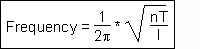where n is the number of poles of the motor, T is the restoring torque, and I is the inertia. Determining the resonant frequency of the decaying response after a step allows us to solve for T. 
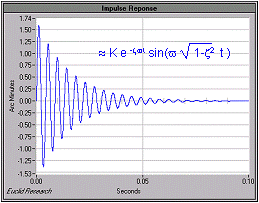If we ignore the non-linearity of the holding torque and distortions caused by the torsional compliance of the couplings connecting the encoder to the motor, the time domain impulse response (derivative of the step response) of the stepper motor can be approximated by the equation:
where K is a scaling factor, 
is the damping factor, and 
is the resonant frequency in radians. Although the frequency can be estimated from the impulse response graph (estimated at the zero crossings), that measurement will be in error by the damping factor adjustment 
. For resonances like the one shown to the right, is small (< 0.1) so its effect on the estimation of the true frequency is negligible.
It should be noted that you must consider the inertia of the shaft, the couplings and the shaft measuring encoder itself when computing the total inertia of the system, I.
Holding Torque Varies With Position
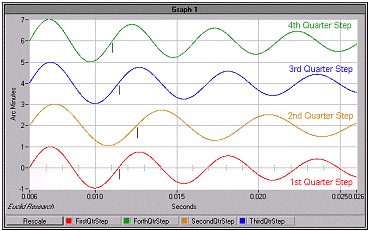The holding torque of a stepper motor is not constant with position but varies as the shaft moves from one full step position to the next. This variation is caused by the detent torque which adds and subtracts from the electrically induced torque as the shaft of the motor moves. The detent torque can be approximated by a sinewave torque that repeats every full step of the motor.
As illustrated to the right, the resonant frequency changes (in response to the changing torque) as the motor is quarter stepped from a full step reset position.
Notice how the 1st and 3rd quarter step share the same frequency. This is because the motor has been stepped to a location where the compliance of the detent torque (dT/dØ) is zero. At the 2nd quarter step (half step location), the detent torque is subtracting from the electrically induced torque resulting in a lower frequency. At the 4th quarter step position (the full step location), the detent torque is helping the electrically induced torque resulting in a higher frequency.
Euclid Research · 2 North 1st Street, 6th Floor · San Jose, CA 95113-1201
Tel: (408) 283-9020 · Fax: (408) 283-9029