
 | Measurement of Static and Dynamic Friction |
The Objective
Compute the static and dynamic friction on an unloaded flywheel assembly. In this application, the customer was interested in computing a first order approximation of the friction acting on a flywheel. The model he selected assumed a static friction component plus a viscous component. Other frictional components were ignored.
The Measurement
The flywheel was accelerated to a velocity of 2100 RPM and allowed to coast to a stop disconnected from any loads. During the coast down process, the SensorPlot™ was instructed to acquire a velocity and acceleration measurement every 10mS until the flywheel came to a complete stop.

| Measurement Theory | ||||||
The customer's model of the friction torque is given by: Tf(FlyWheelVelocity) = Tsf + Cd * FlyWheelVelocity.
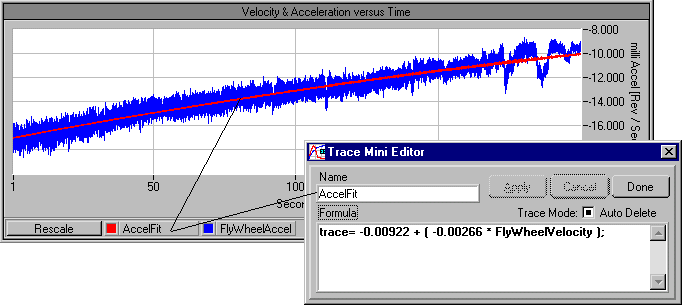
According to this model, the friction on the flywheel is increased, as the velocity of the flywheel is increased. When this function is normalized by the Moment of Inertia (J), the result is an equation for angular acceleration as a function of angular velocity: Acceleration(FlyWheelVelocity) = (Tf / J) = (Tsf / J) + (Cd / J) * FlyWheelVelocity Therefore, if acceleration were plotted as a function of angular velocity, a straight line with a slope of Cd/J and an intercept of Tsf/J would be observed. |
Although it is certainly possible to plot acceleration as a function of velocity to measure/compute the slope (Cd/J), the general data fitting tool of the SensorPlot™ allows one to interactively fit a list of arbitrary equations to a set of plotted data. In this case, the customer simply fit the acceleration curve to a simple combination of a constant and the angular velocity. This is analogous to fitting the acceleration data to an mX + b equation where X is the flywheel velocity. As indicated by the general linear fit tool: (Tsf / J) = 0.00922 and (Cd / J) = 0.00266. Therefore:
| Friction Torque: Tf(FlyWheelVelocity) = -0.0092 * (Inertia) - 0.0027 * (Inertia) * FlyWheelVelocity |
Comments
Angular acceleration is computed by double differentiating angular position. This process is very sensitive to the presence of quantization noise and encoder run-out. The SensorPlot™ uses advanced algorithms that reduce quantization noise. Additionally, a number of tracking filters are available which can be used to remove encoder run-out errors.
Euclid Research · 2 North 1st Street, 6th Floor · San Jose, CA 95113-1201
Tel: (408) 283-9020 · Fax: (408) 283-9029